Understanding fundamentals of imaging lenses

A number of factors should be taken into account when deciding which lens is the best choice for a particular application. In many fairly straightforward applications, only basic systems parameters need to be considered when making the lens selection. However, with ever-increasing demands being placed on imaging systems, many more-complex applications are arising. These involve a range of factors that must be considered to build a system that will perform with high levels of accuracy and reliability.

The fundamental parameters of a system need to be specified to solve almost any imaging application. This kind of information is available from the manufacturer in some form for all lenses.

Field of View (FOV):The FOV is the viewable area of the object under inspection. In other words, it is the portion of the object that fills the camera’s sensor. The FOV can be specified as a range, such as 10-50 mm in the case of a zoom or varifocal lens; as an angular specification, such as 25° for lenses that work over a wide working distance; or as a fixed number, such as 25 mm in the case of fixed-magnification lenses. However, all of these specifications are subject to change if different sized imaging arrays are used.

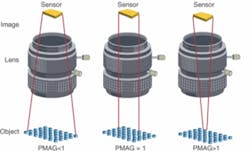
Keep in mind that there are many different sized arrays available on the market, and the physical dimensions of the arrays will need to be known to select the right lens for your application. As the arrays get larger, the FOV increases; conversely, as the sensor gets smaller, so does the FOV. Using the magnification of the lens, you can specify the FOV to take into account different imager formats. The magnification of the lens is the primary magnification of the system and is referred to as PMAG.

Figure 1. PMAG is a property of the lens and describes how much of an object will be seen on a given sensor array. Using the magnification of the lens, you can specify the FOV to take into account different imager formats.

Primary Magnification (PMAG):PMAG describes how much of an object will be seen on a given sensor array and is conveyed by

PMAG = sensor size/FOV
or
FOV = sensor size/ PMAG

Ultimately, we are looking for a lens that meets the FOV needs when coupled with a selected camera. The formula can be solved to tell us what magnification lens is required or what field of view can be obtained as the magnification or the sensor size is varied. Again, you must know your sensor size-also called chip or sensor format-to use these formulas. For example, when

desired FOV = 12.8 mm
horizontal sensor dimension = 6.4 mm
PMAG = 6.4 mm/12.8 mm
PMAG = 0.5X

Or when

desired FOV = 12.8 mm
horizontal sensor dimension = 8.8 mm
PMAG = 8.8 mm/12.8 mm
PMAG = 0.69X

Every lens will have a PMAG or a PMAG range that it will produce regardless of the sensor size that is used, since PMAG is a property of the lens (see Fig. 1). It should be noted that lenses focusing at distances approaching infinity will have PMAGs approaching zero. In these cases, angular field-of-view values can more easily be used to determine FOV. Keep in mind that the angular field will change as the sensor size changes:

FOV = 2 × (working distance ×
tan [θ/2])

whereθ = the angular FOV of the lens for a specific imager size

Imaging-sensor formats:The aspect ratio for many imaging arrays is 4:3 (see Fig. 2). Note that the sensor format size is not equivalent to the sensor’s active area. Video lenses generally can be used with any camera if the lens design format is larger or equal to that of the camera. If the sensor is too large, vignetting (tunnel vision) will occur. For this reason, most lenses will specify a maximum format, or maximum diagonal, with which the lens can be used.

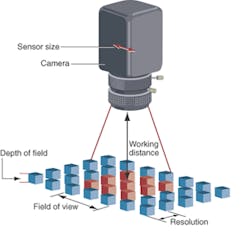
Working Distance:The working distance is the distance from the front of the lens to the object under inspection (see Fig. 3). Some lenses, such as objective lenses, have a fixed working distance; many lenses will have a working-distance range. While this is probably the most straightforward parameter to specify, one must consider a few details when determining the best working distance for an application. Overall, system size, moving parts, flying debris, and lighting all need to be considered when considering the working distance. Additionally, the higher the magnification of the system the longer the lens system will be. If high magnification is required at a long working distance, the system size can increase even more.

Figure 3. The working distance is the distance from the front of the lens to the object under inspection. The minimum feature size of the object under inspection is the resolution. The depth of field of a lens is its ability to maintain a desired amount of image quality as the object is positioned closer to and farther from best focus.

Resolution:The minimum feature size of the object under inspection is the resolution. This is the specification that drives many of the decisions regarding the selection of the camera and lens for a particular application because the resolution of the system in many ways constrains the system’s accuracy and repeatability. Note that resolution and contrast are directly linked and that not all lenses are created equal in terms of their ability to produce resolution and contrast. While two lenses may have identical PMAG/FOV, working distance, dimensions, and so forth, they may not have the same ability to reproduce contrast levels and resolution detail from the object. There are ways to make comparisons between lenses regarding resolution and contrast.

Depth of Field (DOF):The depth of field (DOF) of a lens is its ability to maintain a desired amount of image quality as the object is positioned closer to and farther from best focus. Depth of field also applies to objects with depth, since high-DOF lenses can image the whole object clearly. As the object is placed closer or farther than the working distance, it goes out of focus, and both the resolution and the contrast suffer. For this reason, DOF only makes sense if it is defined with an associated resolution and contrast.

A standard industry practice is to specify the DOF with a single value calculated from the diffraction limit. Making a genuine comparison between lenses is difficult, however, because many imaging lenses are not diffraction-limited. Although two lenses may have the samef/number (such as equal diffraction limit), they do not necessarily have similar performance or comparable DOF. For applications where depth of field is a highly critical requirement, contact the lens manufacturer for the performance capabilities of a lens you intend to use.

GREG HOLLOWS is product line manager, Edmund Industrial Optics, Barrington, NJ,USA; www.edmundoptics.com.