Understanding more pattern-recognition techniques

Understanding more pattern-recognition techniques

MARK A. VOGEL

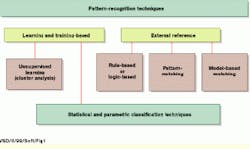
The choice of a pattern-recognition technique depends on whether a trained or an untrained version is more appropriate for the vision task (see Fig. 1). The trainable techniques derive their reference information from a training data set. The alternative approaches obtain their knowledge about classes from an external reference source. These external reference techniques include rule- or logic-based expert systems, pattern- or template-matching systems, and model-based matching systems. An additional technique deals with an unsupervised learning-based cluster analysis that looks in the training data for natural groupings. It can often reveal subclasses and relationships that are not immediately evident.

External references

You can implement the first external reference category--Rule- or Logic-Based--when the classification decision can be easily described by a simple set of rules. Often, these rules for classification are, for example, if the object is smaller than x, round, and red, categorize it as Class 1; if the object is greater than x, elongated, and yellow, then categorize it as Class 2. When complex rules are involved and the computer is performing a task much as a person would, then these rules can be made part of an expert system.

The second external-reference category--Pattern Matching--concerns the recognition of certain constrained objects under controlled conditions. For example, machine-made parts that are manufactured to tight tolerances can be recognized by directly matching the observed object against a stored reference image. If the lighting and geometric conditions of the observation process are controlled and the number of different types of parts that must be recognized is limited, then straightforward template-matching techniques work adequately.

The third external-reference category--Model-Based Matching--is used when the collection of all the observation data necessary to train a standard classifier proves difficult, but modeling the objects of interest is possible because blueprints and specifications are available. Model-Based Matching is used in conjunction with complex simulations of sensor systems and works effectively in overcoming data-collection and observation limitations. For all of these techniques and the trainable approaches, variants and hybridized mixtures have been applied in applications with varying degrees of success.

Trainable recognition

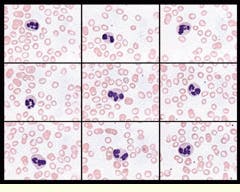
Choosing a specific type of trainable classifier, such as a neural-network classifier, probabilistic classifier, or distance-based classifier, involves a detailed analysis of the imaging application. A typical analysis might deal with the collection of training data (imagery for a vision system) on the objects of interest but where the objects vary because they could be biological in nature or customized during manufacture. Consequently, the quantity of training data that can be collected and the degree of variability of the classes markedly affect the decision process. For example, the type of blood-cell data that can be collected in large quantities is an ideal candidate for trainable classifiers (see Fig. 2).

In general, when more parameters need to be estimated-because more features must be used in the classification process or more classes need to be determined-then, more training data are required. Choosing a simple classifier with a small set of highly discriminative features helps to minimize the data-collection requirements for training. A large neural-network approach with thousands of weights to be learned usually requires orders of magnitude more training data than would a simple minimum distance classifier with a few highly selective features and a few estimated parameters for each class.

If complex feature interrelationships are needed in the classification process, then the minimum-distance approach might not provide the necessary performance. A careful analysis of the observable data and their distributions in each class can be used to determine the complexity of interrelationships.

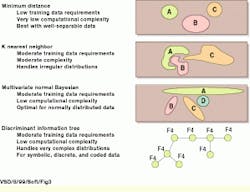
The Minimum-Distance classifier is trained by determining the mean value of each feature in the class (see Fig. 3). New objects are assigned to the class that contains close centers. This classifier is easy to implement, easy to train, and works well when the classes are well separated.

The K-Nearest Neighbor classifier is a powerful method but is computationally more expensive. This classifier assigns new objects to a class based solely on the closest training samples. However, it must sort through many samples to make a decision.

The Multivariate Normal Bayesian classifier is a probabilistic classifier that has certain optimal properties. It is designed to work with features where the class samples have a multivariate normal distribution. In a first estimate, you can check for the typical normal (bell curve) distribution of class data on a feature-by-feature basis.

Lastly, a different type of trainable classifier, the Discriminant Information Tree, looks for an optimal linkage of features in a probability tree structure. It is designed to handle discrete data, such as the shape of an object or the color of an object. In addition, this classifier can use measurement data, such as length, after the data have been quantified or discritized into categories such as small, medium, large, or very large.

For example, if you need to separate long, yellow objects from medium-size red objects, then this type of classifier is appropriate. Sometimes an extensive effort is needed to determine how to best quantify the measurements. However, the main advantages of the Discriminant Information Tree classifier are in exploiting combinations of symbolic and measurement information with complex distributions.

Simple classification

Sometimes you can convert a complex classification problem into a simpler one. Figure 4 shows a two-class problem (left) in which a Minimum-Distance classifier would not work well. A Cluster Analysis (right), which can determine natural groupings, converts the two-class problem into a five-class problem, where the Minimum-Distance classifier can now be successfully applied.

By carefully analyzing an imaging problem, you can select an appropriate pattern-recognition technique. If adequate training data are not available but external sources of information for recognition are available, consider an external reference classifier. If training data are limited, consider a distance or statistical classifier with the estimation of a small number of parameters. If the training data are abundant, class distributions are complex, and computational resources are ample, consider the K-Nearest Neighbor classifier and highly parameterized classifiers such as neural networks. And if the feature interrelationships are complex and symbolic or discrete, consider a technique designed to exploit this data with only a moderate training data burden, such as the Discriminant Information Tree classifier.

FIGURE 1. The type of vision problem, data availability, and pre-existing expert knowledge all play major roles in selecting the appropriate pattern-recognition classifier.

FIGURE 2. The nine data blocks each contain one white blood cell and many red blood cells. Nuclear material is used to stain the white blood cell blue. White blood cells can be classified into a dozen different types, but all of the nine white blood cells belong to the same class. Note that the nuclear material appears in different configurations within each block. This high-within-class variability can be captured by statistical pattern-recognition training techniques.

FIGURE 3. For the Minimum-Distance classifier, classes A, B, and C are well separated, and an assignment of a new observation based on distance to the closest class center would yield appropriate results. When the classes are intertwined, a K-Nearest Neighbor classifier could maintain performance but with higher computational complexity. The probabilistic Multivariate Normal Bayesian classifier uses covariance information to handle classes with significant dispersion and can have optimal performance under proper conditions. The Discriminant Information Tree classifier is demonstrated by the linkage of many features (F1-F8) in its probability structure. It can handle complex distributions of class feature values.

FIGURE 4. Cluster Analysis can locate natural groupings by converting an intertwined complex two-class problem into a less-complex problem with five subclasses.

MARK A. VOGEL is president of Recognition Science Inc. (Lexington, MA); e-mail: [email protected]; www. RecognitionScience.com