Wavelet-based image compression produces less degradation
Wavelet-based image compression produces less degradation
By Andrew Wilson, Editor at Large
In current imaging systems, the massive amounts of digital data that need to be stored pose complex problems for system integrators. In magnetic-resonance scanners, for example, the hundreds of images generated require tens of megabytes of data storage. In remote-sensing systems, where a single satellite image might be as large as 20 Mbytes, terabytes of data are generated.
To meet these storage requirements, system integrators are turning to image-compression software to reduce the
amount of data that needs to be stored, decrease the costs of data storage and image-transmission time. As in other areas of image processing, however, each application demands different types of image compression. Losing any image data through either compression or expansion is generally not acceptable. However, in some storage applications, such as fingerprint data storage, some loss of data information might be tolerated.
Wavelet-based techniques appear to be the most promising methods of compression today. Not only are wavelet techniques relatively straightforward, they can be operated as lossless or lossy encoders and, at present, generate high levels of compression without significant image degradation.
Bi-level images
Several software standards and wavelet- and fractal-compression techniques are available and provide system integrators with numerous choices. The major standards are the Graphics Interchange Format (GIF), Joint Bi-level Image Experts Group (JBIG), and Joint Photographic Experts Group (JPEG).
Based on the Lempel-Ziv-Welch (LZW) compression algorithm, the GIF was originally developed by Compu Serve (Columbus, OH) to compress textual material and files by substituting commonly occurring character sequences that are referenced to the first occurrence of these sequences.
"Although GIF compression is lossless for 8-bit images," says Adrian Vanzyl of Monash University (East Bentleigh, Australia), "it is not suited for 24-bit images. When compressing such images, much of the color information is lost during the quantization process." Furthermore, compression ratios are low and cannot be traded off for compression time or loss of quality.
Like the GIF, the JBIG standard is also designed for lossless image compression. Developed by the International Electrotechnical Commission (IEC; Geneva, Switzerland) and the International Telegraph and Telephone Consultative Committee (CCITT; Geneva, Switzerland), the JBIG standard has been developed for binary (1 bit/pixel) images. However, the algorithm can be used on color images by applying the algorithm one bitplane at a time.
During operation, the JBIG software models the redundancy in the image with correlations of the pixel currently being coded with a set of template pixels from part of the image that has already been scanned. The current pixel is then automatically coded based on this template. Because more bits are assigned to less probable combinations, image compression is achieved.
"Compared to CCITT Group 4, JBIG is approximately 10% to 50% better on text and line art and even better on halftones," says Mark Adler of the California Institute of Technology (Pasadena, CA). "However, JBIG is like Group 4--somewhat sensitive to noise in images--so that compression decreases when the amount of noise in the image increases."
Enter JPEG
Unlike the JBIG standard, the JPEG standard was not developed to handle 1-bit/pixel or moving pictures. Like JBIG, though, the JPEG standard can be used in lossless mode. With lossless compression, all the image information is retained, thereby allowing images to be reliably reconstructed. In this mode, the compression factor for typical images is about 2:1.
More often, though, JPEG is operated in lossy mode, which allows the system integrator a choice of compression ratios. In operation, JPEG uses the discrete cosine transform (DCT) to transform an 8 ¥ 8 block of pixels into frequency-domain coefficients. These coefficients represent successively higher-frequency changes within the block in both x and y directions. Each frequency component is then divided by a separate quantization coefficient, rounded to the nearest integer, and coded with either Huffman or arithmetic coding. Changing the quantization coefficients then determines the level of compression that can be achieved.
"Quantization selectively in creases or decreases the amount of information used to render an image," says Andrew Watson of the Human Systems Branch of NASA Ames Research Center (Moffett Field, CA). This selective allocation is based on the anticipated sensitivity of the human eye to the target portion of the image.
"If the eye is sensitive to the targeted portion," adds Watson, "then more picture information will be used." In JPEG techniques, an averaging approach is taken to determine the eye`s sensitivity to brightness and contrast. This approach leads to an over allocation of information in portions of the image where the eye is not as sensitive as represented.
Because of this, Watson has modeled the sensitivity behavior of the human eye and incorporated the quantizer into a JPEG-like software package called DCTune. According to Watson, the net result is consistently better image quality and higher compression efficiency. Because JPEG can efficiently compress images with minimum loss, it suits applications in which a small data file represents a larger image in database applications (see Fig. 1).
Because 8 ¥ 8-pixel quadrants are often used in JPEG compression, compressed images can exhibit a "blockiness" that could be undesirable in some applications. For this reason, Eastman Kodak Co. (Rochester, NY) chose not to use the JPEG standard in the development of its PhotoCD compression scheme. Rather, the company uses a hierarchical decimation technique, which reduces the number of pixels needed to represent the image, and an interpolation function, which restores the pixels.
According to Kodak, this approach avoids the loss of noticeable detail while maintaining a 6:1 image-compression ratio. In addition, this method provides an efficient means to rebuild the image while minimizing redundant data (see Fig. 2).
Despite the artifacts introduced by JPEG, this standard continues to be used in medical imaging systems. AutoGraph International (San Jose, CA) and a major Danish hospital, for example, have used JPEG to compress digitized film images to as high as 50:1 without endangering the diagnostic quality. However, even though the Digital Imaging and Communications in Imaging standard now supports the use of all modes of JPEG compression, legal issues remain (see Vision Systems Design, Sept. 1997, p. 34).
In Denmark, x-ray-exam results are put in the written report of the radiologist, and any image--compressed or not--must exhibit what is described in such a report. In other countries, however, legal issues abound.
Because the DCT requires high precision to be exactly reversible for integer data, the JPEG committee developed a separate algorithm for lossless compression of image data. In lossless mode, the difference between each pixel is stored, and compression ratios of about 2:1 can be achieved. These factors have therefore led researchers to investigate more efficient methods of compression using wavelets and fractals
Wavelet compression
Unlike JPEG compression, which uses a cosine transform to generate frequency-domain coefficients, the discrete wavelet transform can use a number of wavelet functions localized in both frequency and time. Like the JPEG algorithm, the wavelet transform preserves the original data in the form of coefficients. During operation, a signal or image is multiplied by the wavelet transform, and the transform is computed separately for different parts of the signal (see Vision Systems Design, Feb. 1998, p. 46).
Because the wavelet transform is localized, it can be used to analyze and compress image data without the windowing effects that result from the use of the cosine function in the DCT algorithm. Several different wavelets, including Morlet, Mexican Hat, and Haar, have been used for image analysis and compression.
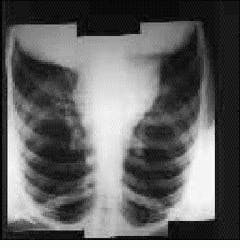
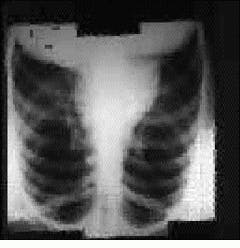
At the Space Telescope Science Institute (Laurel, MD), Richard White has used the Haar transform to compress the preview images in the Hubble Telescope Data Archive. During processing, the wavelet transform is used first and is then followed by quantization to discard noise in the image. Next, the quantized coefficients are coded using a quad-tree approach. According to White, wavelet techniques yield good compression of astronomy images and take about one second for compression or decompression on a Sun Microsystems Sparc Station 2 workstation (see Fig. 3). "Because the calculations are carried out using integer arithmetic," says White, "the program can be used for either lossy or lossless compression, with no special approach needed for the lossless case."
Although other wavelet transformations, such as Daubechies or biorthogonal wavelets, are more complex, they produce better results than the simple Haar transform. Indeed, the availability of several wavelet transforms makes it possible to look for a best-matched wavelet to handle special image data. This matching can be accomplished using either a wavelet look-up table or by developing a specialized wavelet function.
Fractal compression
In 1977, Benoit B. Mandelbrot published The Fractal Geometry of Nature, in which he theorized that fractal geometry was a better method to represent real-world objects such as coastlines and clouds. As a branch of mathematics now known as iterated function theory, Michael Barnsley, a cofounder of Iterated Systems (Atlanta, GA), popularized the technique for image compression.
In March 1988, Barnsley applied for and was granted a second patent on an algorithm that can automatically convert an image into a Partitioned Iterated Function System, which also compresses the image in the process. Using this type of algorithm, Iterated Systems has produced Fractal Imager and Fractal Viewer software packages that can be downloaded from the company`s Web site (www.iterated.com).
Fractal Imager and Fractal Viewer software products create Fractal Image Format (FIF) files using the Fractal Transform process, in which the input image is systematically searched for matching patterns. Initially, the entire image is divided into regions called domain blocks. For each domain block, another region in the image is selected that closely matches the domain, which is called the range block. Range blocks are usually larger than domain blocks and can be rotated or reflected to more closely match the domain blocks.
The location of the range-block transformation to the domain block and statistics about the data are the only information saved in the FIF file. Therefore, the image is stored in terms of itself and its fractal properties instead of containing data for each and every pixel. Because this process requires fewer bytes, images are often expressed as FIF files to achieve compression.
"What fractal-image compression offers is an advanced form of interpolation," says John Kominek of the University of Waterloo (Canada). "This is useful for graphic artists, for example, or for printing on a high-resolution device."
System integrators of image archival and transmission systems have still other factors to contemplate than which compression technique to choose. Standardization, lossless versus lossy, legal issues, flexibility, and expandability are important issues that must be closely examined.
FIGURE 1. By incorporating the behavior of the human eye into the quantizer, JPEG image compression can reach high levels of compression with little loss of detail. This example shows an original image (top) and a JPEG compressed image at 100:1 (bottom).
FIGURE 2. Rather than choose JPEG compression, Eastman Kodak chose a hierarchical decimation technique to compress images in its PhotoCD scheme. This series of images (from left to right) is compressed with the JPEG technique. The original 1.18-Mbyte file was compressed at 9:1, 13:1, 18:1, and 22:1 compression ratios. On the far right is an image compressed with Kodak`s PhotoCD technique. The image was originally a 4.5-Mbyte image file of 1024 ¥ 1536 pixels that was compressed to an Image Pac file of 1.5 Mbytes.
FIGURE 3. Using the Haar wavelet, Richard White and his colleagues at the Space Telescope Science Institute have compressed preview images used in the Hubble Data Archive. The original image (top) has been compressed at 100:1 (bottom) using this technique.