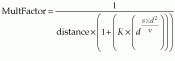Understanding image enhancement

Understanding image enhancement

Peter Eggleston

The image-processing techniques most often implemented by vision-systems designers are enhancement operators. These operators are designed to improve the quality of images to facilitate interpretation or inspection. For data-visualization applications, such as in the display of medical images, enhancement operators are often the highest form of processing performed on imaging data. They can improve contrast, remove noise, "bring-out" areas of interest, and accent or suppress certain image characteristics.

As these operators do not function with any "a priori" knowledge of the image, they are limited in terms of restoring a degraded image. Image restoration is a special class of operator that is based on mathematical models of the degradation process. In automated vision systems, enhancement techniques are used to improve the performance of other algorithms commonly used in machine-vision applications, such as segmentation and pattern-recognition processes.

Enhancement operators are frequently classified as a type of filtering, but they belong in their own distinct class. This is because image filtering blocks or passes a set of frequency components. On the other hand, image-enhancement operators are mostly concerned with a particular operation and do not affect the frequencies contained in an image.

Noise removal

A widely used image-enhancement operator is the median filter. This operator is useful for suppressing random noise while preserving edge detail. During imaging, noise may be introduced by the image sensor; the transmission, storage, and digitization processes; or by subsequent modifications. The median-filter operator smoothes the noise in an image, much like a mean or average filter (implemented as a uniform-identity [all 1s] convolution operator [see Vision Systems Design, June 1998, p. 19], and it tends not to blur. Nonblurring is accomplished because the median filter replaces each pixel in the image with the middle value of the pixel`s local neighborhood, instead of the average value of the neighborhood (see Fig. 1).

A lesser known and used image-enhancement operator is the mode filter. This filter works like the median filter, except that it uses the most frequently occurring pixel value rather than the median value. With this filter, the weights provided by a mask kernel are used to determine how many times a neighborhood value is used in the calculation. This approach gives preference to certain data distributions, such as preferential treatment to pixels closer to the center of the neighborhood. Another variant of this approach is the rank-value filter. This operator counts each pixel value within a window using the corresponding weight specified in a mask kernel. It then sorts the values from least to greatest and selects the value at the specified rank or index.

Taking this approach further, the Nagao filter performs edge-enhancement and image-smoothing simultaneously. However, the resulting image often becomes "blotchy-looking" because, while maintaining differences between areas, sections of the image tend to become their local average. The Nagao algorithm operates by determining the direction of the minimum variance, using eight directions (North, Northeast, East, Southeast, South, Southwest, West, and Northwest) from the center pixel. The center pixel is then replaced by the average of the pixels in the direction of minimum variance. This operator is an iterative operator, as multiple passes can be made on the image. Because of its computational intensity, and due to its blotching effects, the Nagao filter is not often used in machine-vision applications.

An alternative method is to individually weigh each pixel`s contribution to the neighborhood average based on measurements taken over a local area. This approach is implemented in an enhancement operation known as the Weymouth/Overton filter. This enhancement tends to remove noise, while maintaining apparent edges around the image, by taking into account the difference between each neighboring pixel value and the central value, along with the spatial distance of the contributing pixel. The filter also uses the variance within the neighborhood of the pixel. It uses a 3 ¥ 3 neighborhood for each pixel to compute a new value for that pixel. Each pixel`s contribution is given by

Contribution = PixelValue ¥ MultFactor

where d is the difference between the neighborhood pixel and the central pixel values, distance is either 1.0 or the square root of 2, v is the second variance of all the pixels in the neighborhood, and K and s are constants inserted by the user based on empirical data.

The sum of the Contribution is divided by the sum of the MultFactor, and the result becomes the new center pixel output value. However, if all pixels in the neighborhood are the same, then the center pixel remains unchanged. The greater the difference between the center pixel and a neighbor pixel, the less effect the neighbor pixel has.

The Weymouth/Overton operator is more complex and, therefore, takes longer to execute than the Nagao, but it does tend to be more sensitive to edges in the data (see Fig. 2). The described filters are useful for removing noise and restoring noise-degraded images, but they operate with no understanding of the degradation that might have occurred.

Restoration filters such as the Weiner filter take into account a known degradation function and introduced noise. To best use such operators, the frequency spectrums of the original image and the noise must be known. If either one is not known, they can still be approximated and varied slightly until the best-looking output image is obtained.

Contrast enhancement

In many imaging scenarios, the lighting of the scene or objects of interest can`t be controlled, resulting in data where some part, or the entire image, is too bright or dark. If only a portion of the dynamic range of the imaging system is used or if there is too large a difference in brightness over the scene, the image can lose viewable detail. Note that the term viewable is used, because in a typical image of 256 gray levels, humans can only distinguish differences of four levels or more. Examples are indoor images taken under poor lighting conditions and outdoor images taken under bright sun and full shade.

The goal of contrast enhancement is to manipulate these gray levels to improve data viewability. In some cases, contrast enhancement is also used to correct nonlinearity in the acquisition system, compacting some parts of the gray scale while expanding others, so that viewing or processing might be more effective.

Contrast can be defined as the difference in gray levels. The simplest contrast-enhancement method is gray-level scaling, whereby the values in the image are remapped. These functions can either be linear or nonlinear. Nonlinear scales can be used to compensate for nonlinear sensors or to place more emphasis (contrast) on a specific area of interest in the data. The simplest linear approach involves multiplying by a gain value and then adding an offset value (either negative or positive)

New Gray Level = Gain ¥ Old Gray Level + Offset

Gain values of less than 1 result in a decrease in contrast; values greater than 1 result in an increase in contrast, sometimes called contrast `stretching.`

PETER EGGLESTON is North American sales director, Imaging Products Division, Amerinex Applied Imaging Inc., Amherst, MA; e-mail: [email protected].

Part 2 of "Understanding image enhancement" will be published in Vision Systems Design, August 1998.

Figure 1. In image enhancement, the median operator is useful for suppressing random noise, while preserving edge detail. It works by first ordering the data in the neighborhood about a pixel, and then replacing that pixel by the median, or center-ranked, value.

Figure 2. Several algorithmic techniques exist to remove noise while preserving edge quality. The effects of some of these techniques can be seen on this image of a fiducial mark (top left). Proceeding clockwise, a 3 x 3 average filter (top center) or blurring removes noise, but spreads the edges. The 3 x 3 median filter (top right) cleans up the image and improves the edge definition. The 3 x 3 mode (bottom left), Nagao (center bottom), and Weymouth/Overton (bottom right) filters derive a more subtle impact on the image, but are more computationally expensive to implement.