Choosing the Correct Microscope Objective: Numerical Aperture and Other Key Factors

Microscope objectives are critical components of high-magnification imaging systems. These intricate assemblies of multiple lenses are responsible for gathering light from an object and forming an intermediate image, which is then either projected onto a sensor or magnified further by an eyepiece.

Microscope objectives can be divided into two primary categories: finite conjugate and infinite conjugate. Finite conjugate objectives behave much like standard lenses, where an image is created when the specimen is positioned at a finite distance beyond the focal point. On the other hand, infinite conjugate objectives necessitate the use of additional optical elements, such as a tube lens, to bring the image into focus. However, infinite conjugate designs allow the integration of further optics like filters, beamsplitters, and polarizers, making these objectives highly favored in high-magnification setups.

When selecting a microscope objective, multiple factors must be considered, including magnification, numerical aperture (NA), and price. Among these, NA tends to hold the greatest sway, especially when comparing objectives of equal magnification, as it is often viewed as a direct measure of performance. However, it is important to recognize that NA does not tell the whole story, and solely relying on this factor can lead to an incomplete assessment of an objective’s imaging capabilities. This article delves into what defines a microscope objective’s performance and how these factors come into play when creating high-magnification optical systems.

Defining Numerical Aperture

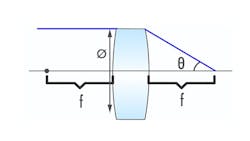
Numerical aperture (NA) is one of the most critical specifications for a microscope objective because it determines the objective's ability to gather light at a given working distance. It describes the acceptance cone of an objective defined by the angle θ and relates to resolution (Figure 2).

Equation 1 below is the first-order formula used to determine NA:

NA = n * sin(θ) [1]

Where:
n = the refractive index of the medium between the lens and the object
θ = half of the objective's angular aperture

Many people equate NA with resolving power, but this is an oversimplification. While it can serve as a proxy for resolution, NA only provides insight into the objective's ability to resolve detail on axis, or at the center of the field of view. Overall image quality can be significantly different off axis.

Equation 2 below establishes the relationship between an imaging system’s on-axis resolution and NA, defining the minimum distance at which two distinct point sources of light can be differentiated.

Resolution = λ/(2*NA) [2]

Where:

λ = wavelength

What Influences Numerical Aperture?

1. Aperture Diameter

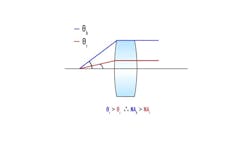
One of the main factors affecting the NA of a lens is its aperture size. A lens with a larger aperture will have a higher NA, as it captures light from a wider angular range (θ). As seen in Figure 3, a lens with a broader angle θ_b will have a larger NA compared to one with a narrower angle θ_r. This enhanced light collection increases both resolution and brightness, allowing the system to capture finer details more effectively.

2. Focal Length

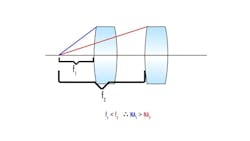
Focal length also plays a crucial role in determining how much light an objective lens can gather. When comparing two lenses of the same diameter, the lens with a shorter focal length will have a larger NA due to the wider angle (θ) it captures. Conversely, as focal length increases, θ decreases, resulting in a lower NA. Figure 4 illustrates this effect, where the shorter focal length f1 allows more light to enter compared to the longer focal length f₂.

Real-World Performance vs. Theoretical Predictions

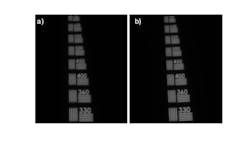
To illustrate the effect of NA in practical scenarios, let us consider two 5X objectives with an NA of 0.14. Their imaging performance was tested using a USAF resolution target, comparing both on-axis and off-axis results. The theoretical diffraction limit, calculated using Equation 2, predicts a resolution of 2.1 µm, equivalent to 238-line pairs per millimeter (lp/mm). Both objectives exceeded this theoretical limit on-axis, achieving high contrast at frequencies above the diffraction threshold.

However, the performance off-axis revealed clear differences between the two objectives (Figure 5 and Figure 6). While they had identical specifications, one objective experienced a dramatic drop in contrast and resolution in the off-axis regions, no longer resolving the same frequencies it could handle on-axis. This disparity highlights that NA alone is not enough to assess the complete performance of a microscope objective, as off-axis behavior plays a significant role in overall image quality.

Several factors can explain why real-world performance often deviates from the theoretical predictions provided by NA calculations. As discussed earlier, the equations commonly used to predict performance are not valid off-axis. The aberrations present in different objective designs could cause two objectives with identical on-axis performance to differ significantly off-axis.

Secondly, theoretical models typically assume monochromatic light, while in practice, broadband light sources are used. Shorter wavelengths in the visible spectrum provide higher resolution, while longer wavelengths decrease resolving power.

Finally, manufacturing tolerances—small imperfections in the production and assembly of the lens system—can also impact the alignment of the lens elements, reducing the objective's overall performance.

Application in the Life Sciences

In many life sciences applications, such as microscopy and high-throughput imaging, it is essential that off-axis performance is maintained. This ensures the entire field of view retains sharpness and contrast, enabling researchers to capture accurate data across the full image. Even if a lens is designated as having "Plan" objectives, which implies that it meets the minimum ISO 19012-1 standard for image flatness, it may not have the same uniform performance across the field. Therefore, it is important to test objectives in real-world conditions rather than solely relying on advertised specifications.

Conclusion

When selecting a high-magnification microscope objective, it is essential to go beyond simply comparing specifications like numerical aperture. While NA can give a general idea of on-axis performance and is very important for these systems, it does not provide the full picture. Factors not accounted for in NA such as aperture size, focal length, wavelength, and real-world off-axis resolution must also be considered. Testing each objective in real-world conditions is critical to ensure that it will meet the demands of the intended application, especially in fields like life sciences, where high image quality across the entire field is crucial for obtaining reliable data.